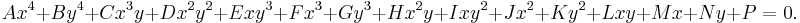Quartic plane curve

A quartic plane curve is a plane curve of the fourth degree. It can be defined by a quartic equation:

$Ax^4%2BBy^4%2BCx^3y%2BDx^2y^2%2BExy^3%2BFx^3%2BGy^3%2BHx^2y%2BIxy^2%2BJx^2%2BKy^2%2BLxy%2BMx%2BNy%2BP=0.$

This equation has fifteen constants. However, it can be multiplied by any non-zero constant without changing the curve. Therefore, the space of quartic curves can be identified with the real projective space 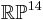$\mathbb{RP}^{14}$ . It also follows that there is exactly one quartic curve that passes through a set of fourteen distinct points in general position, since a quartic has 14 degrees of freedom.

A quartic curve can have a maximum of:

Four connected components
Twenty-eight bi-tangents
Three ordinary double points.

Examples

Bicorn curve
Bullet-nose curve
Cartesian oval
Cassini oval
Deltoid curve
Hippopede
Lemniscate of Bernoulli
Lemniscate of Gerono
Lüroth quartic
Klein quartic
Spiric section
Toric section
Kampyle of Eudoxus